Involute of a Circle Parametric Equations

By Ra_Fiona296 10 Apr, 2022 Post a Comment

For the parametric equation of the involute of the circle. Its been established that the parametric equations of a circle involute are.

Involute Of A Circle Derive Parametric Equations And Find Arc Length Youtube

B Find the points on the curve where tangent is horizontal or vertical.

. The involute of a unit circle is given by the parametric equations xtheta cos theta theta sin theta and ytheta sin theta - theta cos theta theta greaterthanorequalto theta. In this video I go over an example on Calculus with Parametric Curves and this time describe the involute of a circle as a pair of Parametric Equations. The curve traced by the point at the end of the string is called the involute of the circle.

The a displaystyle a term is optional. X Rcos ty Rsin t Find the derivatives of x and y with respect to the parameter t. For a Circle with the parametric equations of the circle and their derivatives are given by.

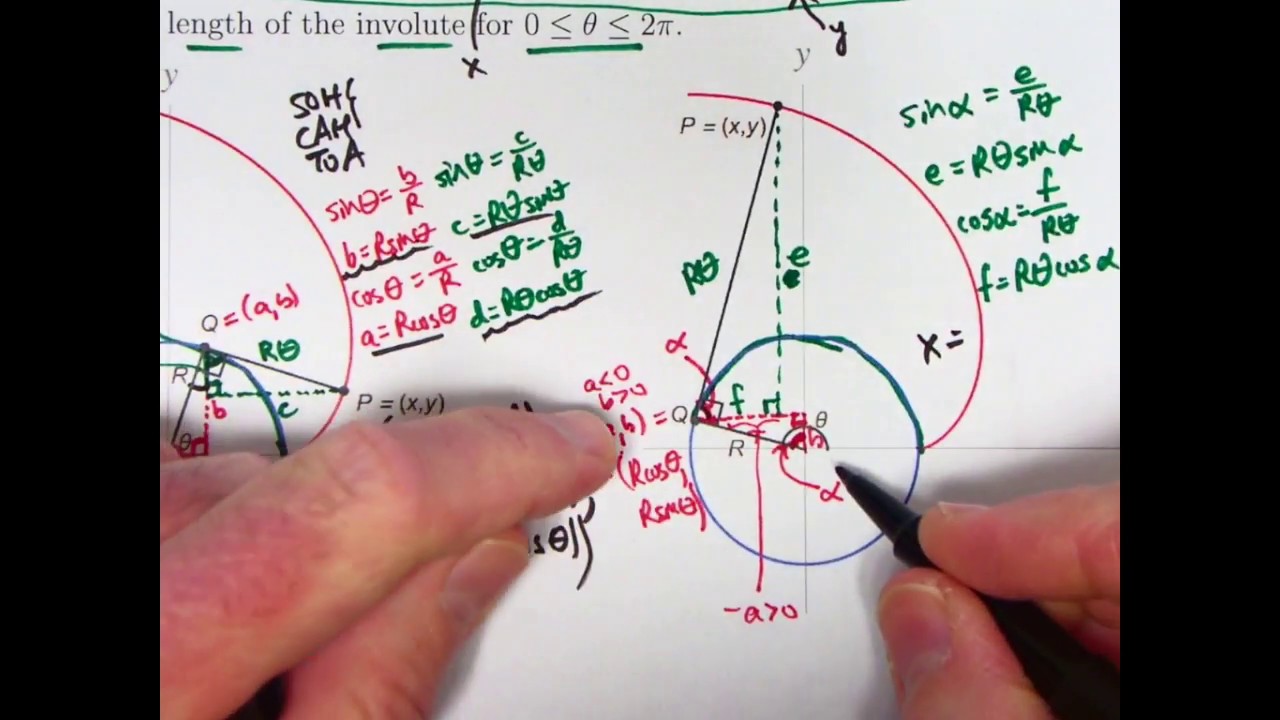
X r cos t y r sin t where xy are the coordinates of any point on the circle r is the radius of the circle and. If the circle has radius and center and the initial posi-tion of is and if the parameter is chosen as in the ﬁgure show that parametric equations of the involute are t P P r Or 0. X a cos t t sin t y a sin t t cos t x acost t sint y asint - t cost x.

Hence the parametric equation for the involute is In the examples of involutes section you will see the derivation of the equation for the involute of a circle as an example. The figure below shows the involute belonging to the base circle with the radius r bA point P on this involute can be described by the angle α which is spanned between the straight lines GP and GT. A Find an equation of the tangent line to the curve when 0 74.

For the calculation of involute gears the involute tooth flank must first be described mathematically. 1 2 The Tangent Vector is. The figure shows involutes for a 05 displaystyle a-05 green a 0 displaystyle a0 red a 05 displaystyle a05 purple and a 1 displaystyle a1 light blue.

4 so the involute is given by. In this video I go over an example on Calculus with Parametric Curves and this time describe the involute of a circle as a pair of Parametric Equations. UsethefollowingFormulastocalculatethedimensionsofthefourcircles needed NisagivenValuePApitchangleisagivenvalueandPDPitchDiameter aregivenvalues PNPDa1P DbPDcosPA ODPD2a DRPD2bwherebhtawhereht2157P 2.

These values are nearly the sine and cosine of the angle t from the unit circle definition of sine and cosine. 2 The involute of a unit circle is given by the parametric equations 0 cose sin and y0 sin 6 cos 6 a 0. In other words for the involute of a unit circle we have textstyle fxy xcossqrtx2y2-1 ysinsqrtx2y2-1 -1 and for the involute of a general circle we have fxyafxaya.

X r_b cospsi psi sinpsiy r_b sinpsi - psi cospsi These equations specifically define an involute for a circle positioned at 0 0 and the involute base starting at a polar angle of zero in the xy plane. Rogawski and Adams Multivariable Calculus 3rd Edition. It resembles an Archimedean spiral.

Because the radius is 1 the center of the wheel has coordinates t 1. The derivatives of these are just. An involute curve can be expressed by parametric equations in planar coordinates.

The unwound portion of the string is tangent to the circle at Q and t is the radian measure of the angle from the positive x-axis to segment OQ. Of the point P xy for the involute. For a circle of radius a x acost 1 y asint 2 the parametric equation of the involute is given by x_i acosttsint 3 y_i asint-tcost.

It serves to set the start location of the curve on the circle. Involute of a Circle Parametric Cartesian equation. Derive the parametric equations.

Segment is arclength per degree of the circle being unwound 2PIR SEGMENT 2 PI REF_R 360. We seek to write the coordinates of the point on the rim as t Δ x 1 Δ y where Δ x and Δ y are as shown in figure 1042. Right angle triangle A Radius B ArcLength.

T is the parameter - the angle subtended by. The image on the left shows the Involute of a Circle. The involute of a circle is the curve formed by tracing the path of the end of string as it is being unwound from the circle while being held taut or pulled tight so there is no.

4 The arc length curvature and tangential angle are st 12at2 5 kappat. B Find the points on the curve where tangent is horizontal or vertical. Beginalign x r costheta theta sintheta y r sintheta - theta costheta endalign where r is the radius of the circle and theta is angle measured from the horizontal.

A string is wound around a circle and then unwound while being held taut. Ref_r is the fixed radius of circle being unwound. 3 and the Arc Length along the circle is.

A Find an equation of the tangent line to the curve when theta pi4. Httpsamznto30sZTSzMultivariable Calculus Challenge Problems Playlist. Write the equation of the circle in parametric form.

Involute Equation Physics Forums